Reatância Indutiva: Fórmula e Cálculos e Mais

Qualquer indutor resiste às mudanças de uma corrente alternada e isso resulta em apresentar uma impedância a ela.
_______________________________________________________________________
Nosso tutorial sobre indutância inclui:
Indutância | Símbolos | Lei de Lenz | Auto indutância | Cálculos de reatância indutiva | Teoria da reatância indutiva | Indutância de fios e bobinas | Indutância Mútua | Transformadores
_______________________________________________________________________
Um indutor resiste ao fluxo de uma corrente alternada como resultado de sua indutância. Qualquer indutor resiste a uma mudança na corrente como resultado da Lei de Lenz.
O grau em que o indutor impede o fluxo de corrente é devido à sua reatância indutiva.

A reatância indutiva é dependente da frequência – aumentando com a frequência, mas pode ser facilmente calculada com fórmulas simples.
REATÂNCIA INDUTIVA
O efeito pelo qual o fluxo de corrente de uma corrente alternada ou variável em um indutor é reduzido é chamado de reatância indutiva. Qualquer mudança de corrente em um indutor será impedida como resultado da indutância associada a ele.
A razão para esta reatância indutiva pode ser vista simplesmente examinando a auto-indutância e seu efeito dentro do circuito.
Quando uma corrente variável é aplicada a um indutor, a auto-indutância dá origem a uma tensão induzida. Esta tensão é proporcional à indutância e como resultado da lei de Lenz a tensão induzida é no sentido oposto à tensão aplicada.
Desta forma a tensão induzida irá trabalhar contra a tensão fazendo com que a corrente flua e desta forma irá impedir o fluxo de corrente e diz-se que o indutor tem uma certa reatância indutiva.
FÓRMULAS DE REATÂNCIA INDUTIVA
Embora não existam indutores perfeitos, é útil imaginar um olhar para as fórmulas e cálculos associados a indutores e indutância. Neste caso, um indutor perfeito é aquele que possui apenas indutância e nenhuma resistência ou capacitância.
A reatância indutiva de um indutor depende de sua indutância, bem como da frequência que é aplicada. A reatância aumenta linearmente com a frequência. Em outras palavras, dobrar a frequência dobrará a reatância indutiva de uma bobina, fio, etc.
É por esta razão que em frequências muito altas, o reativo indutivo para comprimentos de fio se torna importante e, em alguns circuitos, é necessário garantir que as conexões sejam mantidas o mais próximo possível.
É possível expressar isso como uma fórmula para calcular a reatância em uma determinada frequência.

Onde:
XL = reatância indutiva em ohms, Ω
π = letra grega Pi, 3,142
f = frequência em Hz
L = indutância em henries
Leia mais sobre . . . . teoria da reatância indutiva.
LEI DE OHM E REATÂNCIA INDUTIVA
Se um sinal variável, como uma onda senoidal, for aplicado a esse indutor perfeito, a reatância impede o fluxo de corrente e segue a lei de Ohms.
Se o único componente presente for o indutor, então é simplesmente uma questão de aplicar a lei de Ohm e calcular a tensão ou corrente, etc., a partir do conhecimento das outras duas variáveis. Também é possível calcular a reatância a partir do conhecimento da tensão e da corrente.
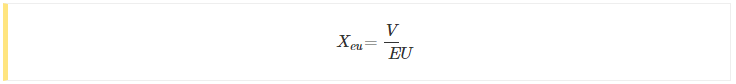
Onde:
X L = reatância indutiva em ohms, Ω
V = tensão em volts
I = corrente em amperes
É possível usar o triângulo da lei de Ohm. Este é um método fácil de memorizar a equação da lei de Ohm. Simples, pegue a variável que deve ser calculada e

O triângulo é usado encobrindo ou destacando a variável necessária. Os dois restantes podem então ser vistos. Se as duas variáveis estiverem próximas uma da outra, elas serão multiplicadas.
Se as variáveis estiverem uma acima da outra, a de cima é dividida pela de baixo. Isso pode ser resumido no diagrama de resumo geral de como o triângulo da lei de Ohm pode ser isizado para reatância indutiva abaixo.
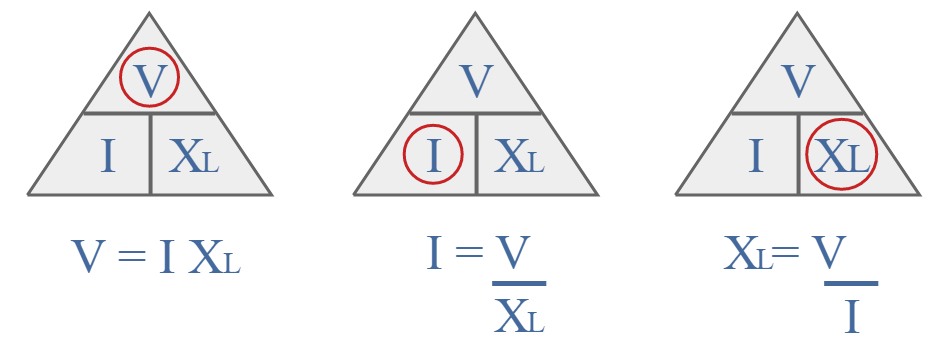
Usar o triângulo da lei de Ohm dessa maneira permite que os cálculos corretos e as versões de fórmula sejam usados para reatância indutiva ao fazer o cálculo do estilo da lei de Ohm.
ADICIONANDO REATÂNCIA INDUTIVA E RESISTÊNCIA
Um indutor real terá alguma resistência, ou indutores podem ser combinados com resistores para formar uma rede combinada. Em qualquer um desses casos, é necessário conhecer a impedância geral do circuito.
Como a corrente e a tensão dentro de um indutor estão 90° fora de fase entre si (a corrente está atrasada em relação à tensão), a reatância e a resistência indutivas não podem ser adicionadas diretamente.
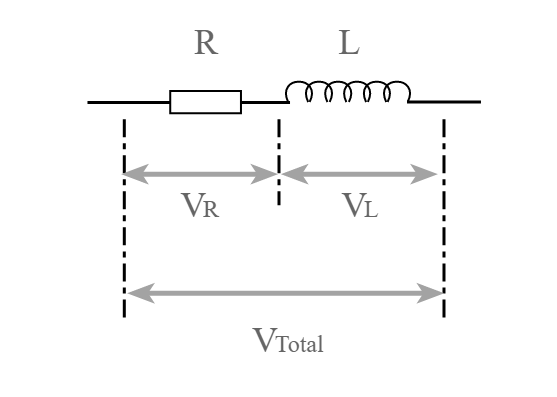

Pode-se ver no diagrama que as duas quantidades precisam ser somadas vetorialmente. Isso significa que a reatância indutiva e a resistência precisam ser elevadas ao quadrado, somadas e, em seguida, a raiz quadrada resultante tomada:

A combinação resultante de resistência e reatância indutiva é chamada de impedância e é novamente medida em ohms.
Ao usar e projetar circuitos que contêm indutores, muitas vezes é necessário observar a reatância indutiva, calculá-la usando as fórmulas acima e adicionar isso a uma resistência pura para obter a impedância geral. Como tal, estas fórmulas são particularmente úteis.
________________________________________________________________


0 Comentários