Fórmulas de Capacitância: Guia Definitivo
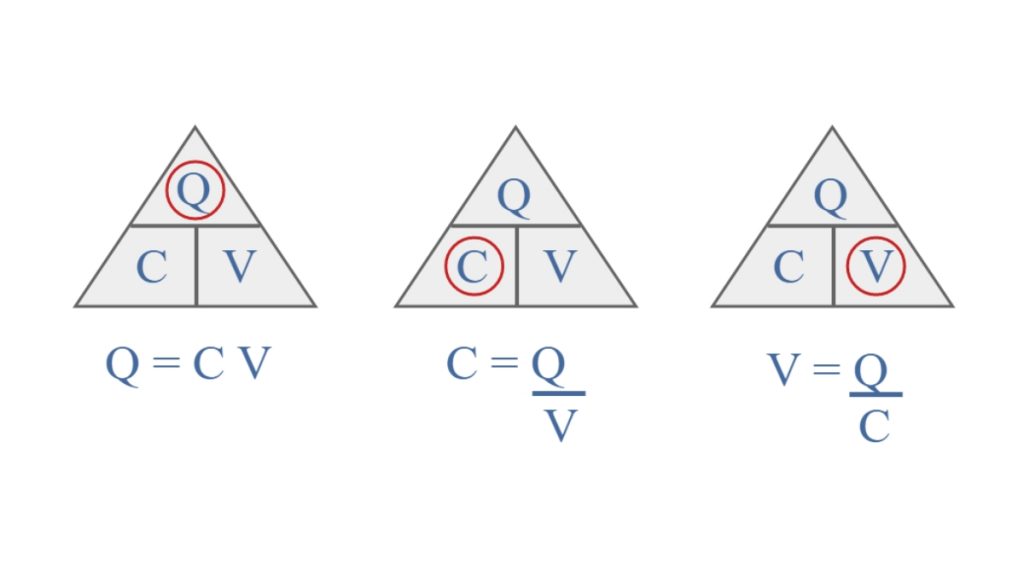
Equações-chave e cálculos para capacitores e capacitância em circuitos eletrônicos, incluindo carga, valor . . .
O tutorial de capacitância inclui:
Capacitância | Fórmulas de capacitores | Reatância capacitiva | Capacitores Paralelos e Série | Constante dielétrica e permissividade relativa | Fator de dissipação, tangente de perda, ESR | Tabela de conversão de capacitores
Existem muitos cálculos e equações associadas aos capacitores. As equações e cálculos de reatância do capacitor são comuns, mas existem muitos outros cálculos de capacitores que podem precisar ser realizados.
Equações de capacitores e cálculos de capacitores incluem muitos aspectos da operação do capacitor, incluindo a carga do capacitor, cálculos de reatância do capacitor de tensão do capacitor e muito mais.

As equações fundamentais do capacitor ou fórmulas e cálculos são muito úteis em várias áreas do projeto de circuitos eletrônicos. Embora possam parecer úteis apenas para situações teóricas e acadêmicas, essas equações e cálculos também podem ser muito úteis em cenários práticos.
Compreender o nível de carga armazenada, as tensões presentes e similares são particularmente úteis.
FÓRMULAS BÁSICAS DE CAPACITÂNCIA
As equações básicas do capacitor ligam a capacitância com a carga mantida no capacitor e a tensão entre as placas.
A capacitância é definida como a capacidade de um componente ou circuito elétrico ou eletrônico de coletar e armazenar energia na forma de uma carga elétrica. É a quantidade de carga elétrica armazenada em um condutor para uma determinada diferença de potencial elétrico.
A partir disso, é possível definir a equação básica para capacitância:

Onde
C é a capacitância em Farads
Q é a carga mantida nas placas em coulombs
V é a diferença de potencial entre as placas em volts
É útil ser capaz de lembrar a equação básica para capacitância. É usado em várias aplicações de projeto de circuitos elétricos e eletrônicos.
Para fazer isso, é útil usar um triângulo de memória semelhante ao triângulo da lei de Ohm, mas usando as variáveis de capacitância.

É muito simples usar o triângulo de cálculo de capacitância. Simplesmente encobrir a quantidade desconhecida e, em seguida, calcule-a a partir das outras duas. Se estiverem alinhados, são multiplicados, mas se um estiver em cima do outro, devem ser divididos.
Por exemplo, se Q é exigido de um conhecimento de C e V, então, porque C e V estão na parte inferior do triângulo, e eles estão próximos um do outro, então podemos ver que Q = C x V.< etc.

O resumo acima apresenta todas as variações da fórmula para que possam ser lembradas com muita facilidade.
Cálculo de Capacitância ou Capacitor de Placas Paralelas
Um dos cálculos básicos importantes associados à capacitância é poder calcular a capacitância de um capacitor de placas paralelas.
Usando as fórmulas relevantes, é possível prever com precisão a capacitância de um capacitor a partir do conhecimento da área das placas, da separação entre elas e da permissividade relativa ou constante dielétrica do material entre as duas placas.
Usando esta equação e teoria básica, também é possível entender os níveis de capacitância parasita em placas de circuito impresso e outros aspectos do projeto de circuitos eletrônicos.
Com as velocidades nos circuitos eletrônicos aumentando rapidamente à medida que a tecnologia para circuitos integrados e similares melhora, os níveis de capacitância parasita das trilhas, etc., tornam-se cada vez mais importantes e podem afetar significativamente a operação do circuito. Assim, é necessário levar isso em consideração para muitos projetos de circuito.
É possível deduzir a capacitância de um capacitor da equação abaixo. As placas devem ser do mesmo tamanho.


Onde:
C = capacitância em Farads
ε r = permissividade relativa para aquele meio
ε 0 = permissividade do espaço e é igual a 8,854×10 -12 F/m
A = área de uma placa em metros quadrados
d = distância entre as duas placas em metros
Determinar a capacitância para um capacitor de placa é muito útil para onde capacitores planos comuns devem ser usados. No entanto, às vezes é necessário determinar a capacitância de um capacitor tubular. Um exemplo disso é quando é necessário determinar a capacitância de um comprimento de alimentador coaxial.

Isso pode ser feito facilmente usando uma versão ligeiramente modificada da fórmula para o capacitor de placa que foi adaptada para acomodar a geometria diferente do capacitor tubular.
C=2 π εr ε0euregistro (umab)C=2π εr ε0llog(ab)
Estes são os casos mais utilizados onde é necessário calcular a capacitância de um item. É possível derivar as fórmulas relevantes para outras geometrias, mas elas tendem a ser mais individuais e pouco utilizadas.
A constante dielétrica e a permissividade relativa são usadas nessas equações. Obter uma maior compreensão. . .
ENERGIA ARMAZENADA EM UM CAPACITOR
Outra equação importante associada aos capacitores é determinar a quantidade de energia armazenada no capacitor.
A energia armazenada no capacitor é igual ao trabalho que foi necessário para estimular a carga no capacitor.
Se a tensão em qualquer instante for “v”, e uma pequena quantidade de carga δq for transferida a essa tensão, então o trabalho realizado será v δq.
Portanto, o trabalho total realizado e, portanto, a energia armazenada no capacitor é:
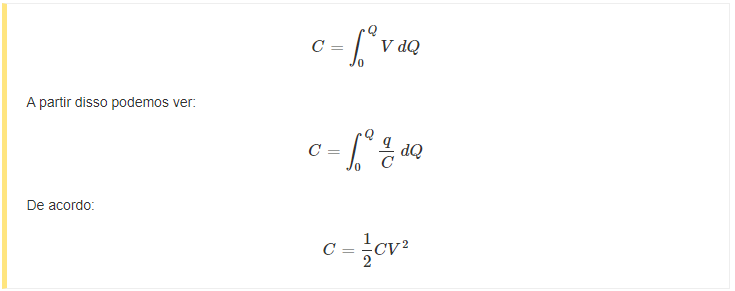
Essas equações e fórmulas são muito úteis em muitas áreas do projeto de circuitos eletrônicos para determinar o nível de carga em um capacitor. Isso pode ser muito importante em muitas situações, incluindo projeto de fonte de alimentação, determinação da capacidade necessária para capacitores usados para situações de interrupção onde a energia pode ser interrompida e muitas outras situações.
As equações básicas para capacitores e sua capacitância permitem calcular os níveis de capacitância, juntamente com a energia armazenada dentro deles. Estas são algumas das principais fórmulas básicas e atributos necessários para a teoria básica do capacitor.




0 Comentários