Forma de Onda Triangular: O que É
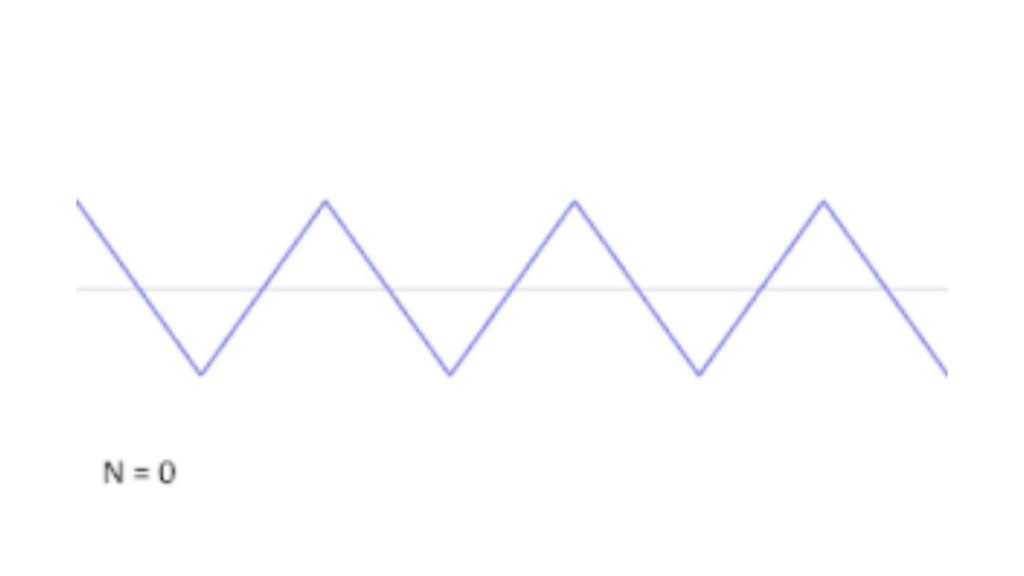
As ondas triangulares são uma forma de onda eletrônica em que o nível de tensão aumenta linearmente e diminui linearmente na mesma taxa para ambas as rampas.
_______________________________________________________________________
As formas de onda eletrônicas e elétricas incluem:
Tipos de forma de onda e fundamentos | Onda senoidal | Ondas quadradas e retangulares | Onda Triangular
______________________________________________________________________
Ondas ou formas de onda triangulares são freqüentemente encontradas em eletrônicos e são usadas para uma variedade de propósitos.
Uma forma de onda triangular consiste em um par de rampas retas consecutivas movendo-se em direções opostas, onde a tensão da variável primeiro se move para cima e depois para baixo. A inclinação da rampa é geralmente a mesma, embora obviamente uma seja a versão negativa ou espelhada da outra.
As formas de onda triangulares podem ser facilmente formadas usando um integrador para dar primeiro uma rampa em uma direção e, depois de atingir a tensão necessária, ele reverte para dar uma rampa na outra direção.

Noções básicas de forma de onda triangular
Para uma forma de onda triangular, as inclinações de subida e descida são geralmente as mesmas. Se nenhuma especificação for fornecida, geralmente é esse o caso. Isso dá à forma de onda um ciclo de trabalho de 50%.
No entanto, é possível ter uma forma de onda triangular não simétrica onde as inclinações de subida e descida diferem.
No caso extremo, o dente de serra assimétrico pode ter uma rampa e uma queda ou elevação muito íngreme ou vertical para dar uma forma de onda de dente de serra.
A forma de onda triangular é frequentemente usada em instrumentos musicais, pois é rica em harmônicos e isso lhe dá um som interessante.
Invista em si mesmo:
Elementos matemáticos da onda triangular
Existem alguns aspectos interessantes na forma de onda triangular e ela tem algumas relações com outras formas de onda.
A onda triangular consiste apenas em harmônicos ímpares da frequência de repetição da forma de onda fundamental, onde a amplitude ou cada harmônico é igual a 1/ (número do harmônico) 2
A onda triangular pode ser expressa matematicamente pela equação abaixo. A equação pode parecer bastante complicada, mas fornece uma representação completa da forma de onda.

Onde
n = 2i-1
A = amplitude da forma de onda geral,
a soma é de i = 1 até o infinito.
A soma faz uso do fato de que -sin(x) = sin(x = π), pois isso lida com os harmônicos ímpares que estão 180° (&pi radianos) fora de fase entre si.
Outro aspecto interessante da forma de onda triangular é que ela é a integral de uma onda quadrada.
Como resultado disso, formas de onda triangulares podem ser facilmente criadas passando uma onda quadrada por um integrador, como um circuito integrador de amplificador operacional. À medida que a onda quadrada alterna entre os dois estados, o integrador primeiro aumenta linearmente e depois diminui.
As formas de onda triangulares são uma das formas de onda básicas frequentemente vistas e processadas como exemplos de tipos de forma de onda. Eles podem ser gerados pela maioria dos geradores de função e podem ser criados integrando uma forma de onda quadrada. Eles também podem ser convertidos em uma representação razoável de uma onda senoidal, passando a forma de onda triangular em um circuito eletrônico que inclui um par de diodos back-to-back. São necessários resistores adicionais para garantir que os níveis estejam corretos para isso.
______________________________________________________________
Mais conceitos básicos de eletrônica e tutoriais:
Tensão | Corrente | Potência | Resistência | Capacitância | Indutância | Transformadores | Decibéis, dB | Leis de Kirchoff | Fator de qualidade, Q | Ruído de RF | Formas de Onda
______________________________________________________________
Retorne ao menu Conceitos Básicos de Eletrônica
A Raisa distribui equipamentos para soldagem e para teste e medição há mais de 30 anos! Considere explorar algumas das nossas principais soluções navegando nas categorias abaixo:



0 Comentários